収束の良い円周率の連分数展開
2012年 12月 02日
前回円周率を連分数展開を利用して求めたが、死ぬほど遅かった。
ということで、今回は違う連分数展開で計算してみよう。
これも、Wikipediaの連分数のところに載っているやつだ。
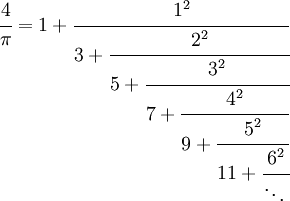
収束が結構良いのが 4/π を連分数で求めるものだ。
4/π=連分数 となっていたので、π=4/連分数 としただけだ。
連分数をそのままfoldrを使って書いてみた。
contfracPi' n = 4 / (foldr (\x y -> 2*x-1+x*x/y) (1%1) [1..n])これで、円周率を求める関数ができた。
実際に計算してみよう。
Prelude Data.List Data.Ratio> let contfracPi' n = 4 / (foldr (\x y -> 2*x-1+x*x/y) (1%1) [1..n])
Prelude Data.List Data.Ratio> contfracPi' 10
11567456 % 3682035
Prelude Data.List Data.Ratio> fromRational (contfracPi' 10)
3.141593167908507
Prelude Data.List Data.Ratio> fromRational (contfracPi' 20)
3.141592653589806
Prelude Data.List Data.Ratio> fromRational (contfracPi' 30)
3.141592653589793
Prelude Data.List Data.Ratio>連分数の計算を、20項あまりまで取ると、精度が浮動小数点の限界に達してしまうようだ。
ちなみに、円周率はこうだ。
Prelude Data.List Data.Ratio> pi
3.141592653589793どうやら、収束はかなり良い気がする。
となると、やはり、円周率を何桁も求めてみたいと思うだろう。
しかし、浮動小数点になってしまうと、精度がすぐなくなってしまう。
いったいどうすれば、100桁、1000桁、10000桁の円周率を得ることができるのだろうか。
分数としては十分な精度が得られているはずなのだが、どうすれば高い精度の10進数に直せるのだろうか。



