これまでのあらすじ
一人二役の寂しいオセロから脱却すべく、オセロの対戦が務まるAIの作成を始めた。
しかし、一通り動きはするものの、このAIは形勢判断を全くせずにテキトーに手を選んでいるだけなので非常に弱い。
なので少しは歯ごたえのあるまともなAIを作ろうと思うのであった。
どうすればまともなAIになるのか
前回作成したAIは
- 取り得る手のうち最も上の行に石が置ける手を選ぶ。
- 同一行に指せる手が複数あるなら最も左の列に石が置ける手を選ぶ。
という単純な実装でした。これには 二つ問題 があります。
- 各手の価値を全く考慮していません。
本来ならばどの手が最も勝利に近付くものなのかを判断すべきです
(「左上に置ける手ほど価値が高い」という誤った判断基準で動いているとも言えます)。 - 現在指せる手しか調べていません。
本来ならば先の先を読むべきです。
オセロは最終的に石の数が最も多いプレイヤーが勝利するため、
終盤は石の数が重要になります。
一方で序盤や中盤は石を取られても後で大幅に取り返すことができるため、
短期的に見て劣勢に見える手が一律に駄目な手とは言えません。
つまり、 これらを解決すればまともなAIになるはず です。
しかし「手の価値」を正確に算出するのは非常に困難です。
ただ 「手の価値」はその手を指した後の盤面の価値から近似できる でしょう。
となると今度は「盤面の価値」をどう測るかという話になってきます。
一先ず今の段階では単純に
- 盤面の価値 = 自分の石の数 – 相手の石の数
としておきましょう。
もう少しまともな算出方法はあると思いますが、
慣れない分野なのでまずは動くものを作ることを優先します。
そうすると残る問題は「先の先を読む」ことになります。
極端な話、「ゲーム開始からゲーム終了まで」を読めば、
勝てる可能性が少しでも残っている限り必ず勝つパーフェクトなAIが出来ます。
しかし、これではオセロで起き得る全ての局面を計算することになってしまい、
まともにゲームが遊べる実行速度ではなくなってしまいます。
何せ4×4という最小限の盤面ですら全局面を読むと待たされたというのに、
8×8の通常の盤面で全局面を読むことは実質的に不可能です。
なので
- N手先まで読んで、その中から最も勝利に近づく手を選ぶ
ことにしましょう。取り敢えずは N = 4 とします。
また、こうしておけば読む手の深さを調整することでAIの「腕前」を簡単に調整できます。
先の先を読む
ゲーム木がある以上、N手先まで読むのは非常に簡単です。
N手先まで探索して見つかった末端のノードに対応する局面を一つづつ調べればいいのです。
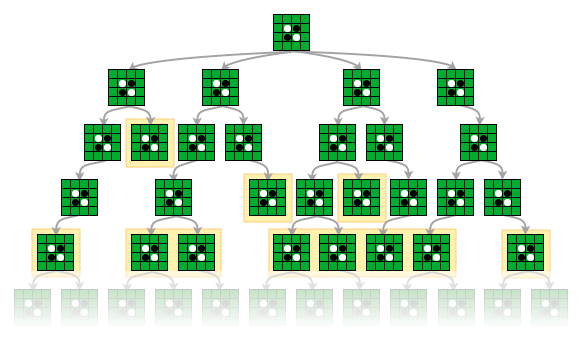
まずは「ゲーム中のある局面から最大でN手先までを切り取る」関数 limitGameTreeDepth を定義しましょう。
これがあれば
形勢判断の処理が
「最大でN手先までを考慮する」ことなく
「最後まで読み切る」形になるため実装が簡単になります。
function limitGameTreeDepth(gameTree, depth) {
return {
board: gameTree.board,
player: gameTree.player,
moves:
depth == 0
? []
: gameTree.moves.map(function (m) {
return {
isPassingMove: m.isPassingMove,
x: m.x,
y: m.y,
gameTreePromise: delay(function () {
return limitGameTreeDepth(force(m.gameTreePromise), depth - 1);
})
};
})
};
}盤面の価値の算出
次に盤面の価値を算出する関数 scoreBoard を定義しましょう。
今回の定義は石の数を数えるだけなので簡単ですね。
まあ「角に置かれた石は重要度を上げる」程度のコツは反映したいものですが、
話がややこしくなるのでそれは将来の楽しみに取っておきましょう。
function scoreBoard(board, player) {
var opponent = nextPlayer(player);
return sum($.map(board, function (v) {return v == player;})) -
sum($.map(board, function (v) {return v == opponent;}));
}
function sum(ns) {
return ns.reduce(function (t, n) {return t + n;});
}手の価値の算出
次に「手の価値」 = 「次の局面の価値」を評価する関数 ratePosition を定義しましょう。
オセロのような二人でプレイするゲームならば
「自分にとって都合の良い手」 = 「相手にとって都合の悪い手」
なので、ある局面の価値は
- もう指せる手が無いなら今の盤面の価値をそのまま手の価値とする。
- まだ指せる手があるなら各手を指した後の局面の価値をそれぞれ求めて、
- 現在の局面が自分の手番ならば、当然最善手を選ぶべきなので、
各手の中から価値が最大の手を選ぶことになる。
ということは「各手の価値の最大値 = 現在の局面の価値」となる。 - 逆に現在の局面が相手の手番ならば、相手も当然最善手を選ぶはずなので、
各手の中から相手にとって価値が最大の手 = 自分にとって価値が最小の手を選ぶはず。
ということは「各手の価値の最小値 = 現在の局面の価値」となる。
- 現在の局面が自分の手番ならば、当然最善手を選ぶべきなので、
という考え方(= ミニマックス法)で定義できます。
function ratePosition(gameTree, player) {
if (1 <= gameTree.moves.length) {
var choose = gameTree.player == player ? Math.max : Math.min;
return choose.apply(null, calculateRatings(gameTree, player));
} else {
return scoreBoard(gameTree.board, player);
}
}
function calculateRatings(gameTree, player) {
return gameTree.moves.map(function (m) {
return ratePosition(force(m.gameTreePromise), player);
});
}最終的な手の選択
後は最も良い手を選ぶ関数 findTheBestMoveByAI を修正すれば完成です。
なお、同じ価値の手が複数あった場合は、
最初に見つかったものを選ぶことにしましょう。
ゲームとして楽しむならランダムに選んでも良いのですが、
動作確認を簡単にするために
「同一局面に対して指す手は常に同じ」
ということにしておきます。
var AI_LEVEL = 4;
function findTheBestMoveByAI(gameTree) {
var ratings = calculateRatings(
limitGameTreeDepth(gameTree, AI_LEVEL),
gameTree.player
);
var maxRating = Math.max.apply(null, ratings);
return gameTree.moves[ratings.indexOf(maxRating)];
}おお……「先の先を読んで最善手を選ぶ」のは難しいことだと思っていましたが、
案外簡単に実装することが出来ました。やりましたね。
遊んでみる
それでは遊んでみましょう!
……う、うーん? 序盤の数手を過ぎると妙に反応速度が鈍くなりますね。
試しに先読みする手数を1に制限してみましょう。

うーん、これだとサクサク動いています。
となると 4手の先読みですら検討すべき局面が爆発的に増えている ということでは……
(実際に計算すると中盤の適当な局面から4手先にあり得る局面は大抵1〜2万くらい存在します)
今回の変更で少しは歯ごたえのあるAIにできたと思ったら、
快適に遊べない状態になってしまいました。
これではAIの強さの変化を実感する以前の問題です。
もっと高速化しなければ……!
次回予告
と言う訳で次回は「AI高速化編」です。



