モンテカルロ木探索で一人不完全情報ゲーム「計算」を賢くする[12]

さて、モンテカルロ木探索が紹介されている情報を探すと、UCTアルゴリズムが紹介されている。 より正確に言うと、UCB(Upper Confidence Bound)によって比較するものである。

詳しくは、いくつかリンク先を紹介しておくので、詳細は自分で調べよう。

1. 「モンテカルロ木探索 並列化、囲碁、マリオAI 」美添一樹
   ちらっと勉強するだけなら、これで十分かな。
2. これで書ける「コンピュータ囲碁講習会」 動画(電通大・イベント), 資料ページ
   2015年の夏に電気通信大学で行われた講習会。ビデオ、資料、ソースコード一式揃ってあるので、必見。
3. 「コンピュータ囲碁 モンテカルロ法の理論と実践」松原仁編
   これが一番まとまっているかな。

さて、成功率だけで評価していたのだが、これはうまく行かなかったのだ。
それで、成功率だけでなく、プレイアウト回数が妥当かどうかも含めた評価値を用意する方法が必要だ。

プレイアウト回数が少ないと、たとえば１回だけだとすると、その１回で失敗していると評価値が非常に悪い。でも、実際にはとても成功率が高いのだが、偶然プレイアウトに失敗しているかも知れない。たった１回の失敗で、そのノードが低く評価され、二度とプレイアウトされないのはとてもまずいことだ。
それで、プレイアウト回数が少ないほど評価値が上がり、プレイアウトする確率が高まるべきである。

で、一気に、UCB値なるものの式を示す。要するに、専門書でちょっと勉強してきた。

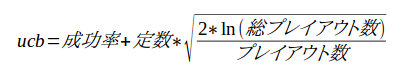
あるノードに対して、札移動を行ってできる全子ノードを考えるわけだが、プレイアウト数が少ないほど評価値を高めるには、プレイアウト数を分子に入れるのは直ぐ考えつくだろう。
単純に、　総プレイアウト数／プレイアウト数　とすると、総プレイアウト数が増加したときの効果が出過ぎるので、理工学ではとてもよくやる手である対数を利用する。
そして、この割合の平方根をとって、適当な係数を掛けたものを成功率に加えてUCB値としている。

定数が０だと今まで通り、成功率だけの評価になる。
定数を増やしていくと、成功率よりも既存のプレイアウトの分布を意識するようになる。
実際には定数を適当な値、たとえば0.5あたりに設定して実行すると良いらしい。

なお、この数式のもっと詳しい意味については、論文もいろいろ発表されているので、自分で調べよう。

これに基づき、特定のノードに対するUCBを計算するメソッドを用意した。
といっても、数式そのまんまなので、何の説明も不要だろう。

double    getUCB() {                  // UCB1
    return    success + UCBCONSTANT * Math.sqrt(2.0*Math.log(parent.playcount)/playcount);
  }

前回と同じ　void playouttree( Node node )　の中を以下のように書き換え、UCB値の最大になるノードを見つけるようにした。

if( node.childmovetype ) {        
        // UCB式に従って枝を選択し、playoutを進める
        double    maxucb = -1;
        for( Node nd : node.childrenpre ) {
          if( nd==null )
            continue;
          double ucb = nd.getUCB();
          if( maxucb < ucb ) {
            maxucb = ucb;
            selectednode = nd;
          }
        }
      } else {

同様に、　void makeMoveBranch( Node parent ) の中も変更した。
移動に対する子ノードを用意するメソッドだが、最初に全子ノードについて１度ずつプレイアウトしており、それでも不足の場合に、さらにプレイアウトを増やすとき、どのノードについてプレイアウトするかについて、UCB値を使っている。

for( ; i<+i ) {
      stock.restore();
      if( list.size()>0 ) {        // 子供がいる場合は、子供のどれかでplayout
        Node maxnd = null;
        double    maxucb = -1.0;
        for( Node nd : parent.children ) {
          double ucb = nd.getUCB();
          if( ucb > maxucb ) {
            maxucb = ucb;
            maxnd = nd;
          }
        }
        maxnd.move.exec();
        double sr = simpleplayout();
        maxnd.addSuccess( sr );
      } else {            // 子供がいない場合は、自身でplayout
        double sr = simpleplayout();
        parent.addSuccess( sr );
      }
    }

UCBへの変更は、たったこれだけで済む。

ということで、早速実行してみよう。
条件は、プレイアウト回数=1000, UCB定数=0.5, 閾値（ノードに対する最大プレイアウト数）=5にて実行してみた。
失敗することも多いのだが、次のように成功することもある。

Game end, rest=0    1/1  1.00000 
Hand:     _ : 
Table:  K  K  K  K 
[1]  
[2]  
[3]  
[4]  

ということで、 プレイアウト回数=1000, UCB定数=0.5, 閾値=5, ゲーム数=100 で実行してみた。つまり、１００回プレイしてみた。

Game end, rest=16    18/100  0.18000 
Hand:     _ : 
Table:  J(Q)  K  8(J)  7(J) 
[1]  TK7Q95JT2K 
[2]  JA 
[3]  K6 
[4]  A4 
----- FINISHED -----

１００回で１８回成功した。まあ、走らせる度に成功率は違うのだが、だいたい20％前後である。

とりあえず、ほぼ成功率が0.0%が、UCBを計算に使うことで一気に上昇した。
いままで、ほとんど成功しなかったものが、ある程度成功するようになったので、劇的な進歩である。
まだ何もパラメータを調整していないので、次回以降、そのあたりを調整することで、成功率の上昇に挑戦してみよう。