よくあるモンテカルロ法による円周率を求めるというのをOctaveでやってみる。
図のように、x,y それぞれ-1〜1の範囲の乱数を生成し、一辺2の正方形と単位円を重ねて、単位円の中に入っている点の割合から円周率を求める。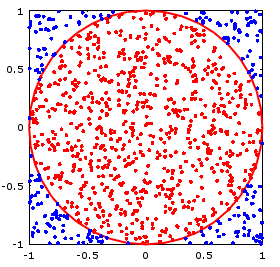
まずは、ごく普通のプログラミング言語風の書き方で試す。
一応、時間を計測するために、time()を使っている。
function [p, t] = pislow( n )
t1 = time();
cnt = 0;
for i=1:n
x = rand()*2-1;
y = rand()*2-1;
if( x^2+y^2 < 1 )
++cnt;
endif
endfor
p = cnt / n * 4;
t = time() - t1;
endfunction
実行すると、こんな感じになる。
精度を上げるために100万回試したら、27秒もかかった。
プログラミング言語としてはかなり遅い方だろう。
>> [p,t] = pislow(1000)
p = 3.1560
t = 0.027001
>> [p,t] = pislow(1000000)
p = 3.1434
t = 27.356
では、Octave的なプログラムにするとどうなるか、見てみよう。
function [p,t] = pifast( n )
t1 = time();
x = rand(n,1)*2-1;
y = rand(n,1)*2-1;
cnt = length(find(x.^2+y.^2<1));
p = cnt / n * 4;
t = time() - t1;forループが消え、100万個の乱数の配列x,yを作って、配列同士の演算をしている。
findは、条件を満たす場合の添え字の配列を返すので、その個数をlength()で数えることで、条件を満たす点数をカウントしている。
これを実行すると、100万回の場合、340倍ほど高速になっている。
これだけの差が出るので、forループを捨てて、配列演算をどんどん使う重要性が分かるだろう。
つまり、forループなどを使わず、配列演算を利用して短く高速に、バグが入る余地も少なくして横着に高速なプログラムを書くのがOctave風なのだ。
>> [p,t] = pifast(1000)
p = 3.1160
t = 0.0010002
>> [p,t] = pifast(1000000)
p = 3.1421
t = 0.080005
でも、注意すべきことがある。配列演算はとても高速なのだが、配列を確保するので、メモリをどんどん消費する。
要素数100万個の配列で、1要素が8バイトだと、1つの配列で8MB消費する。
1000万だと80MB、1億だと800MB、10億だと8GBにもなってしまい、実際に走らすとシステムが反応しなくなる。
最後に、最初に示した図を描くプログラム(スクリプト)を示そう。
hold on;
n = 1000;
x = rand(n,1)*2-1;
y = rand(n,1)*2-1;
lt = find(x.^2+y.^2<1);
ge = find(x.^2+y.^2>=1);
plot(x(lt),y(lt),".r");
plot(x(ge),y(ge),".b");
th = 0:pi/20:2*pi;
plot(cos(th),sin(th),"linewidth",2,"color","red");
hold offhold on; hold off; があるが、これはFigureの重ね描きを制御するためである。
findで、引数の条件を満たす添え字の並びが得られるが、これを元の配列の引数として与えると、条件を満たす要素(値)だけ抽出することができる。これを利用して、条件を満たす場合と満たさない場合をplotを2回使って色分けして表示している。



