偏微分方程式を解くために、まず、行列のreshapeを理解しないといけない。
評価したい対象領域をNNに区切ったので、対象領域はNNの行列(2次元の配列)になっている。実際には温度のN*N配列である。
しかし、温度が行列のままだと、C * T = B という感じで、偏微分を差分表現したのを行列演算に持ち込めない。
なお、Cは係数行列、Tは温度、Bは差分表現の右辺あるいは境界条件である。
そこで、行列を列ベクトルにすることを考える。
行列を整形する関数は非常にたくさんあるのだが、今回使うのはreshape()である。
>> A = 1:9
A =
1 2 3 4 5 6 7 8 9
>> A = reshape(A,3,3)
A =
1 4 7
2 5 8
3 6 9
>> A = reshape(A,9,1)
A =
1
2
3
4
5
6
7
8
9
>>したがって、 C * T = B において、元々2次元配列であったTとBを1次元列ベクトルにできるはずだ。
求めたいのは温度Tなので、C * T = B の両辺にCの逆行列をかけると次のようになる。
T = C \ B
差分表現の右辺あるいは境界条件をNNの行列として作る。 外周以外は、偏微分方程式が成り立ち右辺が0なので、zeros()で全部0のNNの配列を作る。
外周は温度を外気温T0=300を指定するのだが、過熱している辺についてだけ、sinカーブになるようにする。
そして、最後に、N*Nの列ベクトルbを作っている。
B = zeros(N,N);
B(1,:)= B(N,:)= B(:,N) = T0;
B(1:N,1) = sin(pi*x/L)*(TH-T0) + T0;
b = reshape(B,NN,1);
これに合わせて、前回 gallery(“poisson”,N) で作った行列うち、上記の行列Bで温度を指定した箇所に対応する行を、単位行列の行と同じにするために、単位行列の対応行をコピーするという強引な方法をやっている。
C = full(gallery("poisson",N));
I = eye(NN);
C(1:N,:) = I(1:N,:);
C(1:N:NN,:) = I(1:N:NN,:);
C(N:N:NN,:) = I(N:N:NN,:);
C(NN-N+1:NN,:) = I(NN-N+1:NN,:);
C = sparse(C);
N=4の場合の係数行列は次のようになる。
前回と比較すると、対角線上に1が並んでいる箇所が元の領域の外周に相当する行を示す。
C =
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
0 -1 0 0 -1 4 -1 0 0 -1 0 0 0 0 0 0
0 0 -1 0 0 -1 4 -1 0 0 -1 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 -1 0 0 -1 4 -1 0 0 -1 0 0
0 0 0 0 0 0 -1 0 0 -1 4 -1 0 0 -1 0
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
次の図で見たほうが分かりやすいだろう。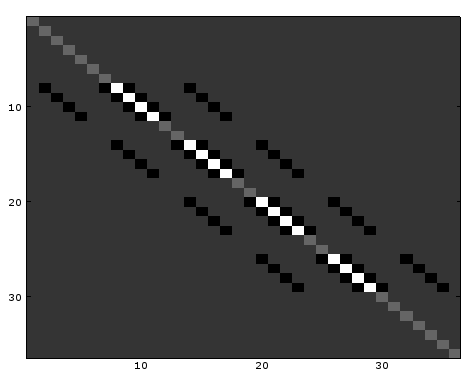
以上で、一通りの説明を終えたので、次回はプログラムを示す。



