Octaveで行列などが扱いやすく数値計算に向いていることは分かったが、結果の数字だけを眺めても様子が分からない。
計算結果を図示することがとても重要だ。図示することで、一瞬でデータの意味が分かる。
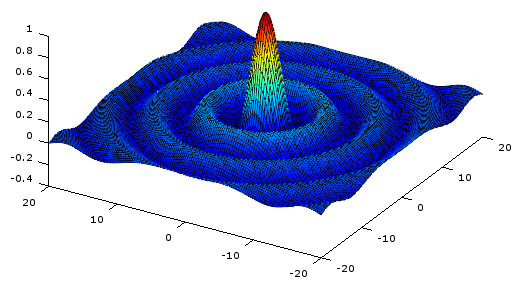
とりあえず、x-y 平面の原点からの距離に応じて高さを決めることで、波を描いてみた。
aは、-20から20までを130等分した配列である。131になっているのは、両端を含む等分点全部となっているため。
meshgridにより、xにはx座標値が入った配列、yにはy座標値が入った配列が作られる。
rには、原点から座標(x,y)までの距離が入るが、epsを加えるというオマジナイをしている。
そして、波の高さをzとして計算している。
面の表示はsurfaceで、メッシュのx座標配列、y座標配列、z座標配列を引数に与えると、上図が現れる。
マウスを動かすことで、好きな方向から眺められる。
次に、もうちょっと複雑な形を作ってみよう。でも、同じくたった5行でできる形だ。
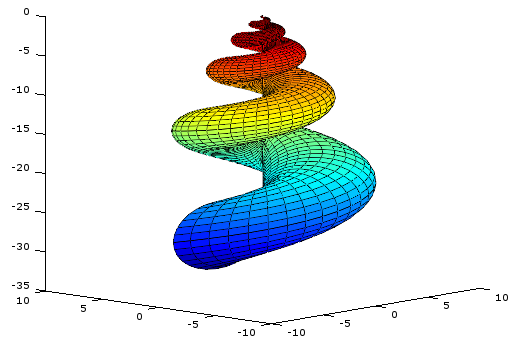 巻貝のような形になっているが、[u,v] の媒介変数で曲面を表しただけである。
巻貝のような形になっているが、[u,v] の媒介変数で曲面を表しただけである。
uは0から10π、vは0から2πのパラメトリック曲面のx,y,z座標値を求めて表示しているだけなので、処理の原理は同じである。
x,y,zの式をいろいろ弄れば、色々な3次元曲面が作れる訳である。
計算結果を図示することがとても重要だ。図示することで、一瞬でデータの意味が分かる。
とりあえず、x-y 平面の原点からの距離に応じて高さを決めることで、波を描いてみた。
>> a = linspace(-20,20,131); >> [x,y] = meshgrid(a,a); >> r = sqrt( x.^2 + y.^2) + eps; >> z = sin(r) ./ r; >> surface(x,y,z);

aは、-20から20までを130等分した配列である。131になっているのは、両端を含む等分点全部となっているため。
meshgridにより、xにはx座標値が入った配列、yにはy座標値が入った配列が作られる。
rには、原点から座標(x,y)までの距離が入るが、epsを加えるというオマジナイをしている。
そして、波の高さをzとして計算している。
面の表示はsurfaceで、メッシュのx座標配列、y座標配列、z座標配列を引数に与えると、上図が現れる。
マウスを動かすことで、好きな方向から眺められる。
次に、もうちょっと複雑な形を作ってみよう。でも、同じくたった5行でできる形だ。
>> [u,v] = meshgrid(linspace(0,10*pi,200),linspace(0,2*pi,30)); >> x = 2*(1-exp(u/(6*pi))).*cos(u).*cos(v/2).^2; >> y = 2*(-1+exp(u/(6*pi))).*sin(u).*cos(v/2).^2; >> z = 1-exp(u/(3*pi))-sin(v)+exp(u/(6*pi)).*sin(v); >> surface(x,y,z);
 巻貝のような形になっているが、[u,v] の媒介変数で曲面を表しただけである。
巻貝のような形になっているが、[u,v] の媒介変数で曲面を表しただけである。uは0から10π、vは0から2πのパラメトリック曲面のx,y,z座標値を求めて表示しているだけなので、処理の原理は同じである。
x,y,zの式をいろいろ弄れば、色々な3次元曲面が作れる訳である。



