誤差が少なくなる級数計算方法で円周率100万桁達成
2016年 11月 24日
Pythonで円周率100万桁の計算をしてきたが、ちょっとだけ誤差がでてしまった。計算の桁数を十分に余裕を持って100万100桁まで計算して100万桁だけ採用すれば、きっと正しい値になるだろう。
でも、これでは面白くない。
あまり余分な桁数まで精度をあげることなく、つまり無駄なく計算をしたいものである。
さて、では、どういう風にやるのが良いだろうか。
各項を項番号nとしたとき、nの式で表した。
そして、n=0,1,2,3,….とやって、項が想定していた誤差epsより小さくなるまで足してきた。
しかし、このやり方は、とても「マズイ」。超高精度計算ではやってはいけない方法だ。
これをちょっとだけ説明しておこう。
ちょっとこんな実験をやってみた。
lamda関数をつい使ってみたが、lambda関数の説明は今回は省略する。とても便利なものだということだけ覚えておいてほしい。
In [30]: term = lambda n:(-1)**n/2**(10*n+6) * (
- 2**5/(4*n+1) - 1/(4*n+3) + 2**8/(10*n+1)
- 2**6/(10*n+3) - 2**2/(10*n+5) - 2**2/(10*n+7) + 1/(10*n+9) )
In [31]: term(0)
Out[31]: 3.1417658730158724term(n)という関数を作って、初項を計算してみたが、すでに3.14…とかなり円周率に近い値になっている。
足し合わせた合計は、ますます円周率に近づくはずである。そして、各項は、どんどん小さくなっていく。
今のプログラムは横着をして、どの項数も同じ精度、有効数字で計算しているのだが、総和は3.14….で、足す数は非常に小さい数である。
足す数の有効数字が100万桁あっても、足された結果は3.14…としたときの有効桁数100万桁になるから、足す数は有効桁数が100万桁でも、桁合わせして足されるため、実際に足した後に反映される桁は一部である。
nが大きくなるにしたがって、実際の有効桁数はどんどん減ってしまう。
これが積もっていくと、誤差が何桁にもなってしまう。
ということで、足し方を変えよう。
前から足してダメなら、後ろから順番に足してみよう。
以下がそのプログラムである。
def FabriceBellard(len):
var('a:z')
term = (-1)**n/2**(10*n+6) * (
- 2**5/(4*n+1) - 1/(4*n+3) + 2**8/(10*n+1)
- 2**6/(10*n+3) - 2**2/(10*n+5) - 2**2/(10*n+7) + 1/(10*n+9) )
eps = 10**(-n).evalf(2,subs={n:len+2})
nmax = 0;
while True:
t = term.evalf(10,subs={n:nmax})
if abs(t)<eps: break="" nmax="" +="1" sigma="0" for="" m="" in="" range(="" nmax,="" -1,="" -1="" ):="" return="" sigma.evalf(len)="" <="" code=""></eps:>最初に、何項になったらepsより小さくなるかを求めて、そこから初項まで逆順に加えている。
これで実行した結果を示す。
In [23]: len = 1000001
In [24]: st = time.time()
In [25]: p = FabriceBellard(len)
In [26]: time.time()-st
Out[26]: 41192.76380801201
In [27]: str(p)[-50:]
Out[27]: '56787961303311646283996346460422090106105779458151'
In [28]: str(sympy.pi.evalf(len))[-50:]
Out[28]: '56787961303311646283996346460422090106105779458151'今回は、項の計算を2回行っているのだが、全体の計算時間は1回しかやらなかった前回よりも短くなっている。こういうところにも、後ろから足した効果が出ている。
計算結果は、sytmpy.pi の100万桁の値とちゃんと一致している。
この計算、もっと桁数をサボりながら100万桁計算することができるが、それくらいは各自でやってみよう。
桁数をどんどん増やしたいなら、はやりPythonでは限界がある。そういう場合は、C言語とかで頑張って欲しい。その場合でも、今回使った円周率の次の公式は役立つはずだ。
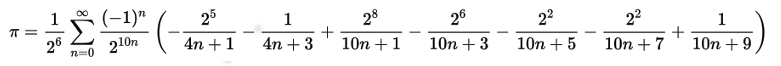
今から40年近く前、8ビットパソコン(マイコン)で1万桁を求めるのが流行ったりしたが、コンピュータの性能はどんどん上昇し、いまや個人でも1兆桁に挑戦できるくらいコンピュータの性能が向上している。
ということで、円周率の話はここで終わりとする。



