データ解析のための統計モデリング入門 一般化線形モデル(GLM) 読書メモ
2017年 02月 14日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第3章、一般化線形モデル(GLM)についてまとめます。
この章では主にポアソン回帰について解説されています。
ポアソン回帰というのは、ポアソン分布の平均がリンク関数という関数を通してデータと関連するモデルを使った回帰です。
モデルが複雑になったので、この回帰で得られる物が何なのかをグラフに描くコードを用意しました。
コードはRで書きました。
linkFunction <- function(b1, b2) {
function(x) {
exp(b1 + b2 * x)
}
}
distribution <- function(x, linkFunction) {
l <- match.fun(linkFunction)
function(y) {
dpois(y, lambda = l(x))
}
}
ps <- 0:10
xl <- "y"
yl <- "probability"
legends <- c("x = 0","x = 5","x = 10", "x = 15", "x = 20")
pchs <- c(0, 5, 10, 15, 20)
for (b1 in seq(-0.1, 0.1, by = 0.05)) {
for (b2 in seq(-0.1, 0.1, by = 0.05)) {
l <- linkFunction(b1, b2)
title <- paste("lambda = exp(", b1, "+", b2, "x)")
plot(0, 0, type = "n", xlim = c(0, 10), ylim = c(0.0, 1.0), main = title, xlab = xl, ylab = yl)
for (x in seq(0, 20, by = 5)) {
d <- distribution(x, l)
lines(ps, d(ps), type = "l")
points(ps, d(ps), pch = x)
}
legend("topright", legend = legends, pch = pchs)
}
}この例では、説明変数xに対してyが分布する場合について考えています。
リンク関数を作るコードは以下のようになります。
パラメータb1、b2を与えると、そのパラメータを使ったリンク関数を返しています。
linkFunction <- function(b1, b2) {
function(x) {
exp(b1 + b2 * x)
}
}リンク関数は引数xを取って、パラメータと足したり掛けたりした後、累乗を計算する関数です。
ポアソン回帰ではリンク関数の戻り値を、ポアソン分布のパラメータとして使います。
リンク関数があれば、あるxに対するyの分布が得られます。
つまり、yを引数に取りyが起きる確率を返す関数が得られます。
以下の関数により得られる関数でyの起きる確率が計算されます。
distribution <- function(x, linkFunction) {
l <- match.fun(linkFunction)
function(y) {
dpois(y, lambda = l(x))
}
}これがポアソン回帰のモデルです。
後はリンク関数で使われるパラメータを最尤推定で求めれば良いわけです。
今はとりあえずモデルの具体例が見たいだけなので、パラメータは自分で与えて、様々な値についてグラフをプロットしてみました。
コードを実行すると、いろいろな場合についてグラフがプロットされます。
具体例として、観ていて面白いのはb1 = -0.1、b2 = 0.1の場合です。
以下に図を貼ります。
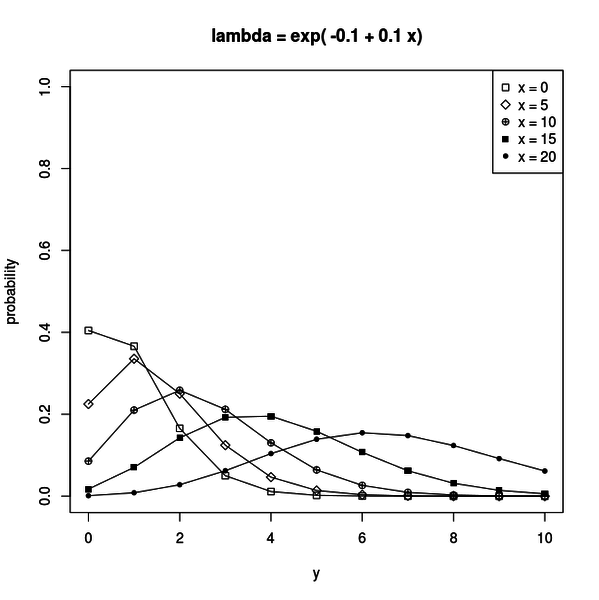
リンク関数はexp(-0.1 + 0.1x)になります。xがある数だった場合、yはこの値を平均に持つポアソン分布で分布するということです。
例えばx = 1の場合は1です。x = 11の場合はe = 2.718...です。
b2が正なのでxが大きくなるほどリンク関数の指数の肩は大きな数になります。
つまり、大きなxではyは大きな平均を持つポアソン分布をします。
図を見ると、確かにxが大きくなるにしたがってyの分布は大きな値を取るようになっています。
このように、ポアソン回帰で得られるのはxの変化によってyの分布がどのように変化するかという傾向です。
ただ変化すると言うだけでなく、どれくらいの分布を伴って変化するかも分かります。



