データ解析のための統計モデリング入門 GLMの尤度比検定と検定の非対称性 読書メモ4
2017年 03月 28日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第5章、GLMの尤度比検定と検定の非対称性についてのまとめの四回目です。
この章では尤度比検定などについて説明がされています。
尤度比検定の手法の一つとしてパラメトリックブートストラップ法が説明されています。
前回はパラメトリックブートストラップ法でどのようにデータがシミュレートされているか見るためのコードを紹介しました。
コードを実行するとグラフが3枚プロットされます。
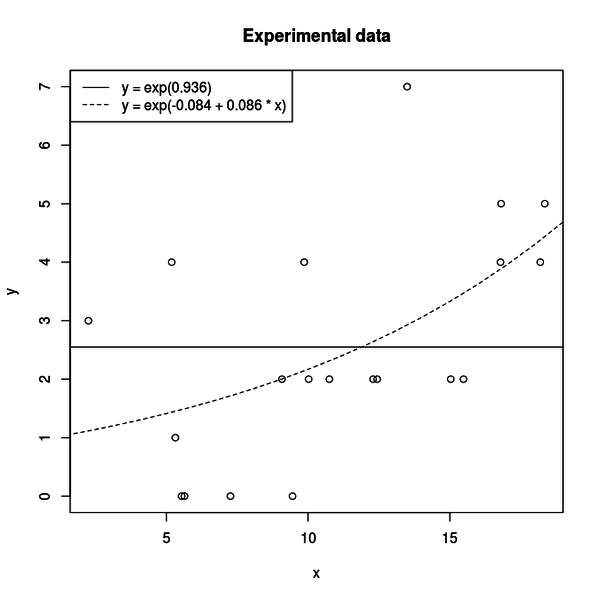
1枚目は以下のような図です。createData を使ってサンプリングしたデータと、帰無仮説と対立仮説に対してポアソン回帰して得られた曲線がプロットされています。
このデータは何かの実験データのような、検定にかけたいデータだとします。
帰無仮説は formula に y ~ 1 を使っている方で、対立仮説は y ~ x を使っている方です。
データは x と正の相関のあるデータなので、対立仮説は右肩上がりの曲線になっています。
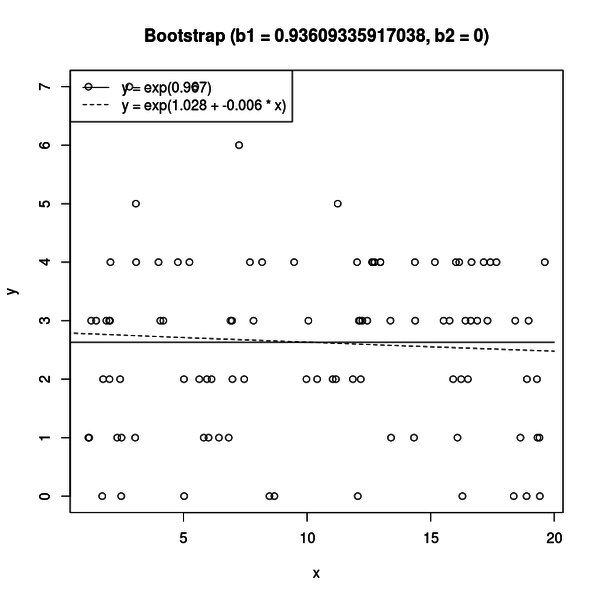
2枚目は以下のような図です。
パラメトリックブートストラップ法で使う、ポアソン回帰で得られた帰無仮説のパラメータを使ってシミュレートしたデータと、そのデータに対して新たにポアソン回帰して得られた帰無仮説と対立仮説の曲線がプロットされています。
帰無仮説は x と相関のないモデルなので、これを真の分布だと仮定してシミュレートすると、得られるデータは x に相関のないデータになります。
すると、帰無仮説も対立仮説も、ほとんど同じような直線になってしまいます。
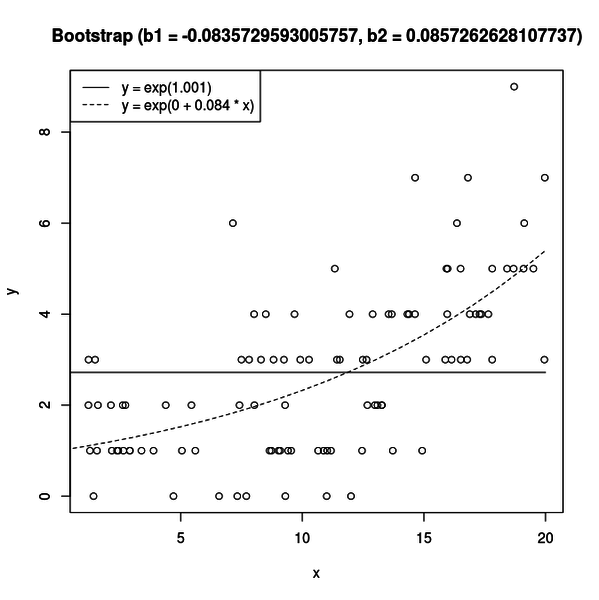
3枚目は以下のような図です。
パラメトリックブートストラップ法ではこういうシミュレーションは行いませんが、参考までに帰無仮説ではなく、対立仮説の方のパラメータを使ってデータをシミュレートして、2枚目と同じようなプロットを作ってみました。
対立仮説は x と相関のあるモデルなので、そのパラメータを使うと x に相関のあるデータがシミュレートされます。
すると、ポアソン回帰で得られる曲線は、実験データの時と同じような曲線になります。
このように、検定にかけたい元の実験データと、パラメトリックブートストラップで行うシミュレーションで生成されたデータは性質が違うデータです。
この違いを利用して尤度比検定は帰無仮説を棄却できるのですね。



