データ解析のための統計モデリング入門 GLMの尤度比検定と検定の非対称性 読書メモ2
2017年 03月 21日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第5章、GLMの尤度比検定と検定の非対称性についてのまとめの二回目です。
この章では尤度比検定などについて説明がされています。
尤度比検定の手法の一つとしてパラメトリックブートストラップ法が説明されています。
前回はパラメトリックブートストラップ法がどのように動くのかを見るためのコードを紹介しました。
コードを実行すると結果は次のようになります。
何度か実行してみて、だいたいの傾向をつかんでみてください。
data size 5 , lambda = exp(0.01 + 0.03x)
P = 0.956
Failling to reject the null hypothesis.
data size 5 , lambda = exp(0.01 + 0.1x)
P = 0.098
Failling to reject the null hypothesis.
data size 20 , lambda = exp(0.01 + 0.03x)
P = 0.128
Failling to reject the null hypothesis.
data size 20 , lambda = exp(0.01 + 0.1x)
P = 0
The null hypothesis is rejected.だいたいの傾向としてサンプル数が多くて x の相関が強いほど帰無仮説は棄却されやすくなります。
データを生成する真の分布は x と相関があるので、帰無仮説は棄却されて欲しいですが、そうならない場合があるわけです。
その様子をグラフにもしてあるので、紹介します。
まずは帰無仮説が棄却されて、無事正しいモデルが支持された場合です。
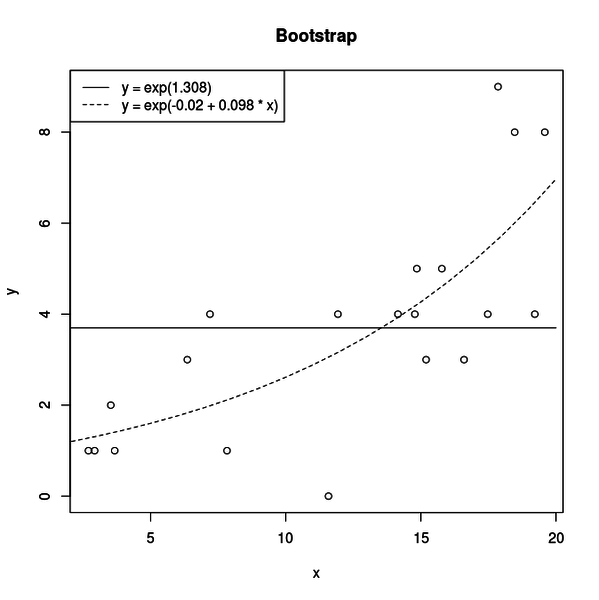
検定に使われたデータが丸、実線が帰無仮説、点線が対立仮設です。
対立仮設の x の係数は 0.098 と推定されています。
おかげで対立仮設は帰無仮説と比べて x と相関のあるデータによく当てはまり、二つのモデルの逸脱度の差が大きくなってP値が低くなり尤度比検定で正しいモデルが選択されたわけです。
一方、帰無仮説が棄却できなかった場合はこのような図になります。
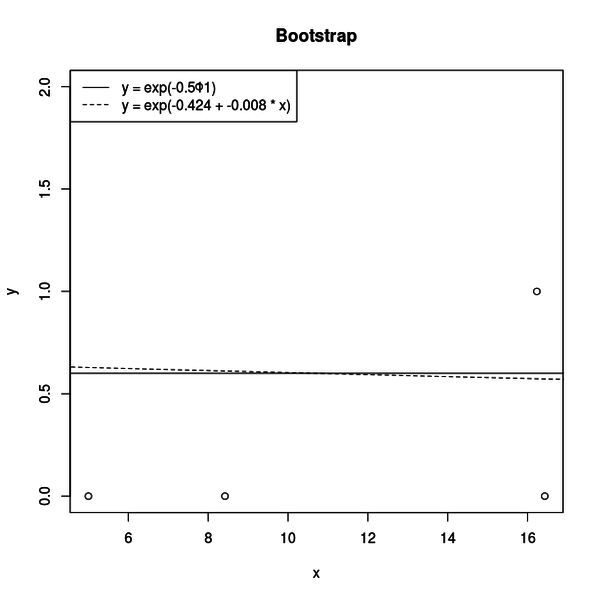
一見して帰無仮説も対立仮設も違いが見えません。
対立仮設の x の係数は 0.008 と推定されていて 0 と違いはほとんどありません。
とすると、帰無仮説でも対立仮設でもデータへの当てはまりの良さに違いはほとんどなく、十分なP値が得られなかったということです。
だいたいの感覚として、帰無仮説が棄却されたりされなかったりする時はこういうことが起きています。



