データ解析のための統計モデリング入門 GLMの応用範囲をひろげる 読書メモ9
2017年 05月 12日
このブログ記事は『データ解析のための統計モデリング入門』(久保拓弥 著、岩波書店)という、とても分かりやすい統計モデリングの入門書を、さらに分かりやすくするために読書メモをまとめたものです。
今回は第6章、GLMの応用範囲をひろげるについてのまとめの九回目です。
この章では様々なタイプのGLMについて説明がされています。
その中でガンマ回帰について説明がされています。
なので、サンプルデータを用意して、ガンマ回帰をやってみるコードを用意しました。
コードはRで書きました。
dataSize <- 1000
createData <- function(createY) {
createY <- match.fun(createY)
x <- runif(dataSize, 0.1, 0.9)
y <- createY(x)
data.frame(x, y)
}
dataGenerator <- function()
createData(function(x) rgamma(dataSize, shape = 4, rate = 4 / exp(0.5 + log(x))))
data <- dataGenerator()
fit <- glm(y ~ log(x), data = data, family = Gamma(link = "log"))
b1 <- fit$coefficients[1]
b2 <- fit$coefficients[2]
phi <- summary(fit)$dispersion
cat("b1", b1, "\n")
cat("b2", b2, "\n")
cat("shape", 1 / phi, "\n")
cat(paste0("rate = ", round(1 / phi, 3), " / exp(", round(b1, 3), " + ", round(b2, 3), " * log(x))\n"))
rate <- function(x) {
1 / (phi * exp(b1 + b2 * log(x)))
}
xs <- c(0.1, 1.0, 2.0, 3.0, 4.0)
ys <- 1:10
title <- "Gamma regression"
xl <- "y"
yl <- "Probability"
legends <- paste0("x = ", xs)
plot(0, 0, type = "n", xlim = c(1, 10), ylim = c(0.0, 1.0), main = title, xlab = xl, ylab = yl)
for (x in xs) {
y <- dgamma(ys, shape = 1 / phi, rate = rate(x))
lines(ys, y, type="l")
points(ys, y, pch = x)
}
legend("topleft", legend = legends, pch = xs)ガンマ回帰のリンク関数は平均を与えるだけで、ガンマ分布のパラメータそのものは得られません。
なので、推定された分布を計算するには、もうひと工夫必要になります。
どうすればいいかはサポートページに書いてありました。
以下のコードがガンマ回帰でリンク関数のパラメータと、ガンマ分布のパラメータを決定するために必要なパラメータを計算している部分です。
fit <- glm(y ~ log(x), data = data, family = Gamma(link = "log"))
b1 <- fit$coefficients[1]
b2 <- fit$coefficients[2]
phi <- summary(fit)$dispersionphi はshapeパラメータと shape = 1 / phi という関係を持つパラメータです。
shapeパラメータが得られれば、rateパラメータは以下のように得られます。
rate <- function(x) {
1 / (phi * exp(b1 + b2 * log(x)))
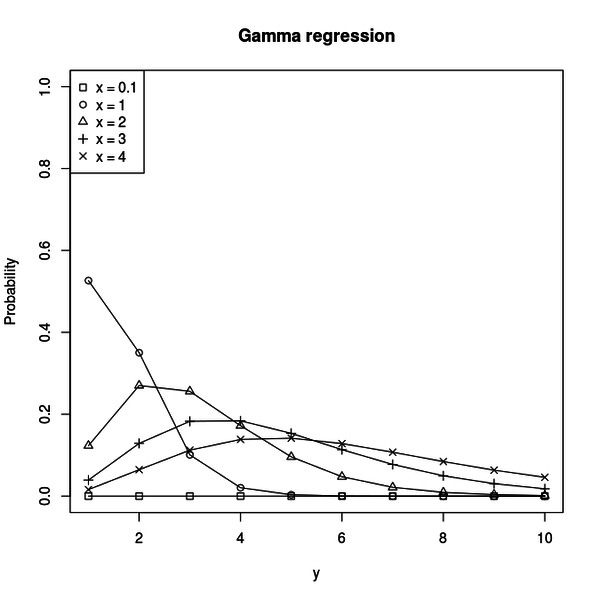
}これで推定したガンマ分布をプロットすることができるようになりました。
コードを実行すると以下のような図がプロットされます。