まだまだ正月気分だと思うので、コンピュータやAI、高尚な数学はじっくり取り組むこととして、簡単な小中学生向けの問題に取り組んでみよう。
【問題】
さて、上記の説明から、半径、頂点のx,y座標値は全て整数としても良さそうな気がする。
整数だけに限定すれば、プログラムが楽になるので、そうしよう。
まだ、3点の場合が求まっただけである。
次回には、6点、10点、さらにもっと多数の点について求めてみよう。

【問題】
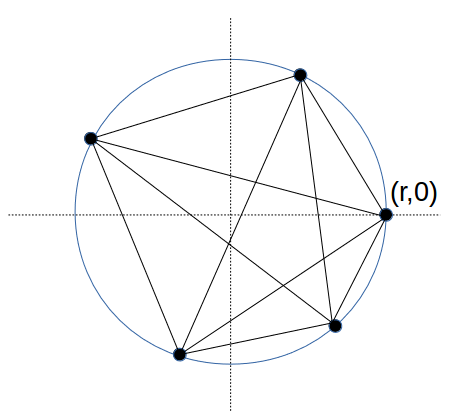
円周上に5点を取り、任意の2点間の距離が整数になる場合の5点の座標を求めよ。
ただし、1点は、半径をrとしたとき、 (r,0) とする。
5点が簡単と思った場合は、点数を増やそう。
たとえば、10点の場合を考えてみよう。
それもさっさとできたら、もっとたくさんの点の場合を考えよう。
そして、一般化してみよう。
ヒントは、「ピタゴラスの定理」である。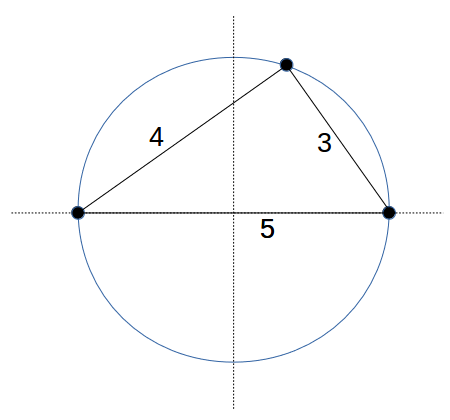

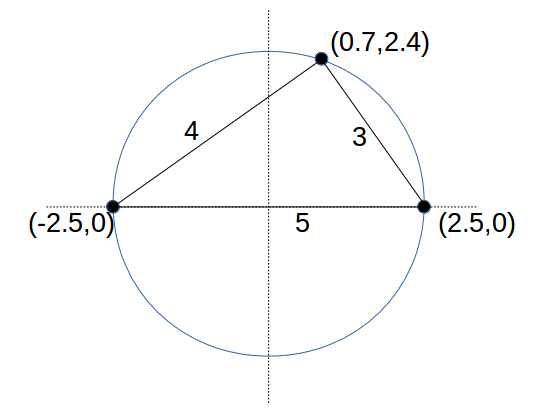
もし、5点ではなく、3点の場合には、3辺の長さが3, 4, 5 の正三角形を考えると良い。
長さ5の辺の端点の1つを(r,0)、つまり(2.5,0)とし、もう一方の端点を(-2.5)とすると、長さ5の辺は、半径2.5の円の直径となる。
そして、もう1つの頂点は、正三角形なのだから、当然円周上になる。
だから、このもう1点の座標を求めれば、3点の場合は決まる。
右の図は、5点の場合を求めるとても良いヒントになっている。
この図をいじっていると、それだけで5点、さらには6点の場合が自然に分かるだろう。
ということで、ぜひ手作業で、あるいはプログラムで解いてみよう。
さらに、もう少しヒントを追加しておこう。

右図に3点の座標を示す。
(2.5,0), (-2.5,0), (0,7, 2.4) である。
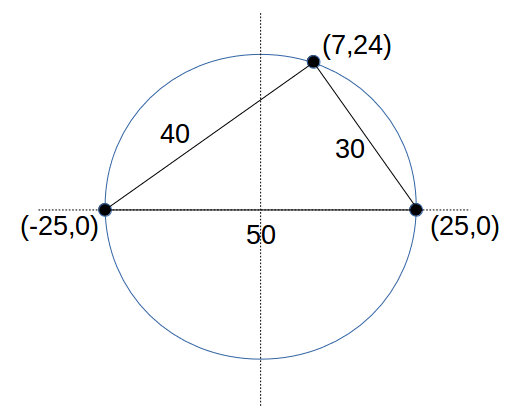
10倍して小数点を取り除くと、
3点は (25,0), (-25,0), (7, 24) となる。

さて、上記の説明から、半径、頂点のx,y座標値は全て整数としても良さそうな気がする。
整数だけに限定すれば、プログラムが楽になるので、そうしよう。
まだ、3点の場合が求まっただけである。
次回には、6点、10点、さらにもっと多数の点について求めてみよう。



