-
 2024.04.09
2024.04.09Rails: 失われたメッセージを巡る冒険
#i18n#ruby#Ruby on Rails -
 2024.01.25
2024.01.25input要素とbutton要素のイベント発火について
#html#javascript -
 2024.01.18
2024.01.18systemd-bootの紹介
#linux#systemd#Windows -
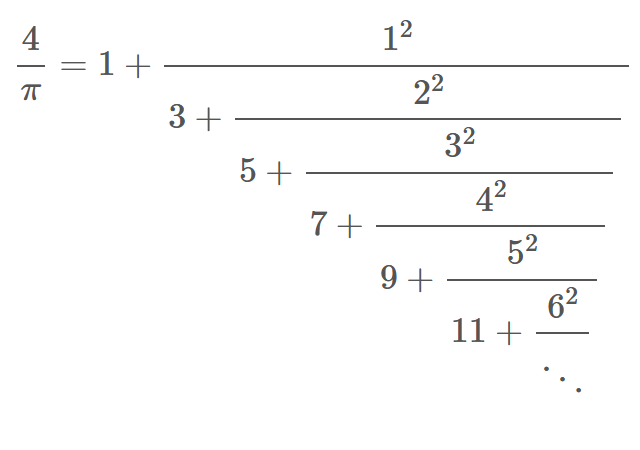 2024.01.11
2024.01.11Julia, 連分数で円周率の計算
#Julia#再帰呼び出し#有理数#畳み込み関数#連分数#高精度演算 -
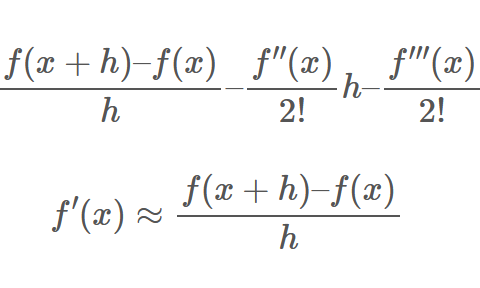 2023.12.14
2023.12.14数値微分の高精度化(下)
#Julia#数値微分#複素数#超高精度計算 -
 2023.12.07
2023.12.07Kaigi on Rails の conference-app に型をつけてみた (中編)
#Kaigi on Rails#rails#rbs#ruby#Ruby on Rails#typing -
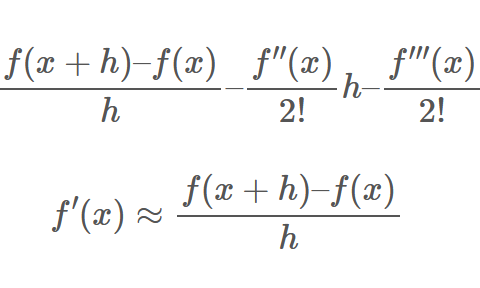 2023.11.30
2023.11.30数値微分の高精度化(上)
#Julia#テーラー展開#差分#数値微分#有効桁数#桁落ち -
 2023.11.24
2023.11.24Rust用PEGパーサジェネレータのrust-pegの紹介 [2]
#parser#peg#rust -
 2023.11.16
2023.11.16Rust用PEGパーサジェネレータのrust-pegの紹介 [1]
#parser#rust -
 2023.11.10
2023.11.10Kaigi on Rails の conference-app に型をつけてみた (前編)
#Kaigi on Rails#rbs#ruby#typing -
 2023.11.09
2023.11.09Python/tkinterでの多角形の作り方(2)
#tkinter#フラット化#マニュアル#可変個引数#多角形 -
 2023.11.06
2023.11.06Kaigi on Rails 2023 参加レポート (@tk0miya)
#Kaigi on Rails#ruby#Ruby on Rails -
 2023.11.02
2023.11.02Rubyの時間を止めるには
#ruby#Ruby on Rails#テスト -
 2023.11.01
2023.11.01Kaigi on Rails2023の参加レポート
#KaigionRails#Ruby on Rails -
 2023.10.26
2023.10.26initial-letter プロパティでドロップキャップを簡単に
#css#CSSプロパティ#initial-letter#Webデザイン -
 2023.10.19
2023.10.19Python/tkinterでの多角形の作り方(1)
#tkinter#入門書#可変長引数#多角形#実用性 -
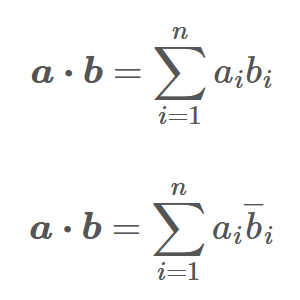 2023.10.12
2023.10.12numpyの内積(5)テンソル積
#Numpy#テンソル積#内積#多次元配列#階数 -
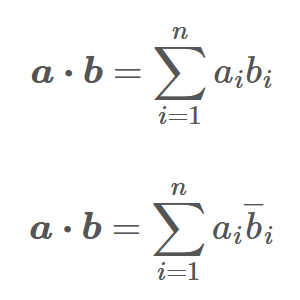 2023.10.05
2023.10.05numpyの内積(4)多次元配列
#Numpy#ベクトル#内積#多次元配列 -
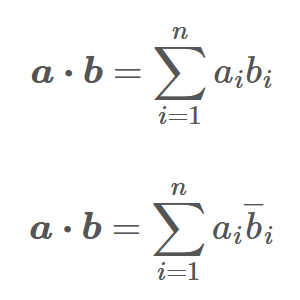 2023.09.28
2023.09.28numpyの内積(3)array like
#LaTeX#Numpy#スカラー#フラット化#内積#線型代数#行列 -
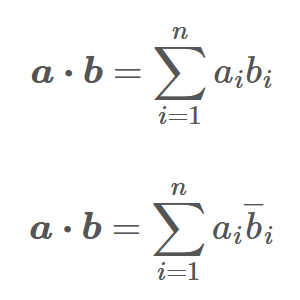 2023.09.21
2023.09.21numpyの内積(2) vdotのソース
#flatten#Numpy#ravel#vdot#仮引数 -
 2023.09.14
2023.09.14RBS の self-type を理解する
#rbs#ruby#Ruby on Rails -
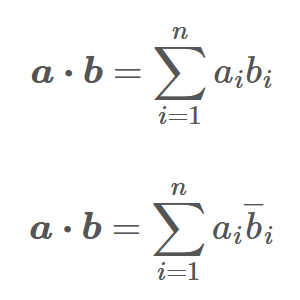 2023.09.07
2023.09.07numpyの内積(1) dotとvdotの違い
#Numpy#vdot#共役複素数#内積#複素数 -
 2023.08.31
2023.08.31組織のGoogleグループ一覧を取得するしくみの作成
#GAS#Google Group -
 2023.08.24
2023.08.24FactoryBot を使って JSON 文字列を生成する
#ruby#テスト -
 2023.08.17
2023.08.17Raspberry Pi スパコン (22) 最終回
#ARM#スパコン#ファン#並列処理#冷却#異音 -
 2023.08.10
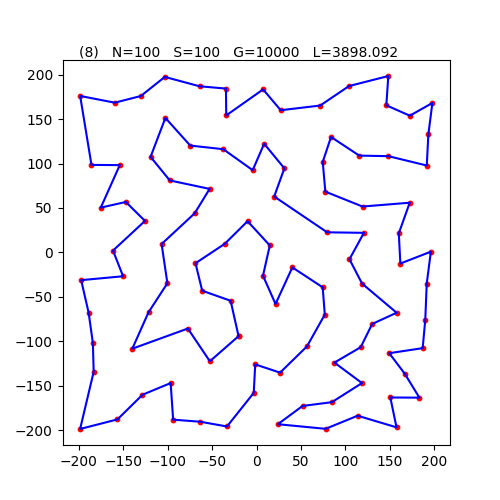
2023.08.10Raspberry Pi スパコン (21) 巡回セールスマン問題
#MPI#局所最適解#島モデル#巡回セールスマン問題#焼きなまし法 -
 2023.08.03
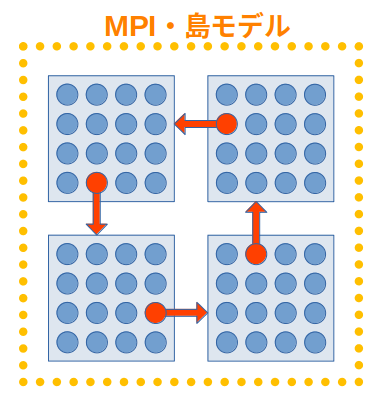
2023.08.03Raspberry Pi スパコン (20) 巡回セールスマン問題
#MPI#世代数#個体数#分散化#島モデル#巡回セールスマン問題 -
 2023.07.27
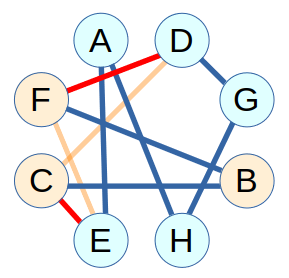
2023.07.27Raspberry Pi スパコン (19) 巡回セールスマン問題
#RNA#ウイルス#巡回セールスマン問題#怠惰#突然変異#遺伝 -
 2023.07.20
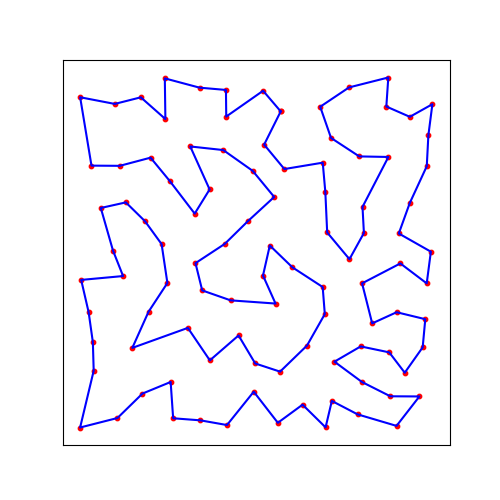
2023.07.20Raspberry Pi スパコン (18) 巡回セールスマン問題
#Raspberry Pi#交差#巡回セールスマン問題#突然変異#進化計算#遺伝的アルゴリズム -
 2023.07.13
2023.07.13Docker container で private gem を利用する
#Docker#rails#ruby#ssh#ssh-agent



