前回、次図のようになった。
Game end, rest=32 0/1 0.00000
Hand: _ :
Table: 8(9) 6(8) 9(Q) J(2)
[1] Q9TTKKA5J85JKQ829QA7KA254TJT6937
[2]
[3]
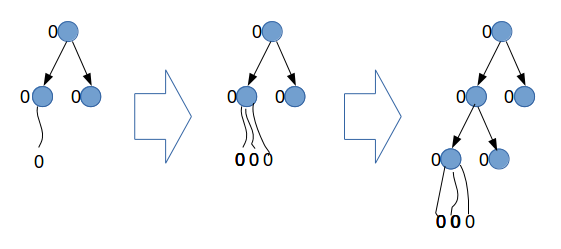
[4]札が屑札[1]に延々と重なるが、他の屑札 の山にはさっぱり重ならないことが分かった。
なぜ、こうなってしまうのだろうか。
まず、プレイアウトだけれど、まだ始まったばかりの状態では、成功率は0に限りなく近い。まあ、常に0が出ると仮定しても問題ないくらいだ。
手札をいずれかの屑札の上に重ねるとき、屑札[1]〜屑札[4]のいずれかの山への移動を行うわけだが、プログラムでは[1]から順番に調べるようになっている。
そして、[1]〜[4]のなかで、そのノード(札移動とノードは対応する)の今までの成功率を調べ、成功率が一番高いノードを選び、そのノードに対する盤面の状態からプレイアウトして、成功/失敗をシミュレーションするのであった。
さて、成功率だが、プレイアウトすると、ほぼ確実に、99.99%の率で成功率0.0となるのだった。
また、まだ一度もプレイアウトしていないノードの成功率は0.0 としているので、選ぼうとしている現ノードの直下のノードの成功率はどれも0.0 の筈なのだ。
全て同じ0.0 の成功率のノードの中から比較して一番成功率の高いノードを選択しているのだが、これが結局いつも最初のノードを選ぶことになっているのだ。
さて、こうなる部分のソースコードを見てみよう。とくに、カードを移動する場合に、どの移動を選択するかの部分に注目してみよう。
void playouttree( Node node )の中の以下の部分が該当する。
if( node.childmovetype ) {
double max = -1;
for( Node nd : node.children ) {
if( nd==null )
continue;
if( max < nd.success ) {
max = nd.success;
selectednode = nd;
}
}
} else {条件判断が、if( max < nd.success ) となっているので、最も大きい最初のノードが選ばれる。
これを、次のように変えてみた。
if( node.childmovetype ) {
double max = -1;
for( Node nd : node.children ) {
if( nd==null )
continue;
if( max <= nd.success ) { // 比較に=を含めた
max = nd.success;
selectednode = nd;
}
}
} else {不等号に=を加えたのだが、同様の比較が成功率を再帰的に書き換える場所にもあるが、全く同様なので説明を省略する。
さて、これで、結果はどうなるだろうか?
最終結果が次:
Game end, rest=23 0/1 0.00000
Hand: _ :
Table: 3(4) Q(A) 8(J) K
[1]
[2]
[3]
[4] 9TKKJ6T9A8K7A744JJ575Q3今度は、最後の[4]がゴミ札だらけになったので、想定通りである。
一応、最初のあたりも載せておく。
Hand: K : 9QJT56789TJQKA23456789TJQKA23456789TJQKA2345678
---- game ---- step 1 success= 0.00000
Hand: T : 9QJT56789TJQKA234567898JQKA23456789TJQKA234567
Table: A(2) 2(4) 3(6) 4(8)
[1] K
[2]
[3]
[4]
---- game ---- step 2 success= 0.00663
Hand: 3 : 9QJT56789TJQKA234567898JQKA23456789TJQKA27456
Table: A(2) 2(4) 3(6) 4(8)
[1] K
[2] T
[3]
[4]
---- game ---- step 3 success= 0.00000
Hand: 8 : 9QJT56789TJQKA234567698JQKA23456789TJQKA2745
Table: A(2) 2(4) 3(6) 4(8)
[1] K
[2] T
[3] 3
[4]
---- game ---- step 4 success= 0.00000
Hand: Q : 9QJT56789TJ5KA234567698JQKA23456789TJQKA274
Table: A(2) 2(4) 3(6) 8(Q)
[1] K
[2] T
[3] 3
[4] 最初は色々な山にバラバラに積まれていくようだが、あるところから最後に固まってしまうみたいだ。
これも、たぶん、どの屑札の山を選んでも成功率が0になり、比較に等号が入ったので、最後が選ばれるようになった結果であろう。
さて、両極端な例が確認できたのであるが、成功率を大いに考慮し、成功率が高いノードでさらにプレイアウトするのはもちんなのだが、成功率が低いとか、まだ一度もプレイアウトされていないノードなども考慮したノード選択をすべきであろう。
というところまで分かったが、実際にはどうすれば良いのだろうか?
何かうまい方法は考案されていないのだろうか?



