モンテカルロ木探索で一人不完全情報ゲーム「計算」を賢くする[15]
2015年 12月 14日
モンテカルロ木探索では、プレイアウトするノードを選ぶ工夫をしていた。
なので、ここでは、プレイアウトするノードを選ぶ工夫を一切止めるとどうなるか試してみよう。
つまり、どの葉ノードも同じプレイアウト回数にするとどうなるだろうか。
ルートノードから指定レベルだけ木を展開し、その末端の全ての葉ノードについて、同じ回数だけプレイアウトしてみよう。
つまり、次図のようなことを試してみよう。
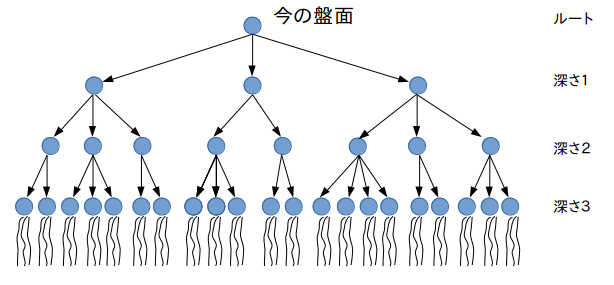
そのために、親ノードと、木を展開する高さ(level)を与えると、子ノードの中で一番成功率の高いノードを親のメンバー変数bestにセットするようにした。
もちろん、このメソッドは、再帰的に呼ばれるようになっている。この、再帰的に行えるということは非常に有利な点である。 モンテカルロ木探索では、それまでの成功率が複雑に影響していたのだが、この単細胞モンテカルロ木探索(これは勝手に命名したものである。正式の言い方があるかも知れない)では、つねに一定回数のプレイアウトしかしないので、ノードの成功率や試行回数などを記録しておく必要もなければ、プレイアウトが終わったノードは除去してもかまわない、とてもメモリにやさしい方法である。
では、プログラムの修正部分を示す。
まず、この単細胞モンテカルロ木探索の核となる再帰的に調べるメソッドを示す。
// 現在の盤面から指定レベル下の葉ノードで、指定回数playoutする
void simpletree( Node parent, int level ) {
Stock stock = new Stock();
if( level == 0 ) { // 指定回数のプレイアウトを行い、成功率を設定し、終了
double successsum = 0.0;
for( int i=0; i<PLAYOUTCOUNT; ++i ) {
successsum += simpleplayout();
stock.restore();
}
parent.success = successsum / PLAYOUTCOUNT;
return;
}
ArrayList<Move> list = getAllTefudas();
boolean istefuda = list.size()>0;
if( list.size()==0 )
list = getAllMoves();
if( list.size()==0 ) {
parent.success = restcount==0 ? 1.0 : 0.0;
return;
}
parent.moves = list.size()==0 ? null : list;
double sumsuccess = 0.0;
double maxsuccess = -1;
Node bestnode = null;
for( Move mv : list ) {
Node nd = new Node( parent, mv );
mv.exec();
simpletree( nd, level-1 );
if( istefuda ) {
sumsuccess += nd.success;
} else {
if( nd.success > maxsuccess ) {
maxsuccess = nd.success;
bestnode = nd;
}
}
stock.restore();
}
if( istefuda ) {
parent.success = sumsuccess/list.size();
} else {
parent.success = maxsuccess;
parent.best = bestnode;
}
}
そして、1ゲームを行うメソッドonegameから呼び出す。
int onegame() {
initialize();
int step = 0;
currentsuccess = 0.0;
for(;;) {
if( tefudatop == 0 )
opentefuda();
Node root = new Node();
simpletree( root, DEPTH );
if( root.moves.size() == 0 )
break;
Node nd = root.best;
currentsuccess = nd.success;
nd.move.exec();
++step;
}
return restcount;
}
モンテカルロ木探索に比べると非常に単純になるのだが、これでも高い成功率が得られるのであろうか?
レベル 幅 成功率 4 20 60/100 0.600 5 20 72/100 0.720 6 20 83/100 0.830 7 20 82/100 0.820 7 50 90/100 0.900 8 2 82/100 0.820 8 20 46/52 0.885 9 3 43/50 0.860 9 5 92/100 0.920
この結果から分かることは、
- 木の高さを増やす
- 幅(葉ノードでのプレイアウト回数)を増やす
結論として、単細胞モンテカルロ木探索でも、どうやら成功率90%くらいは達成することが分かったが、モンテカルロ木探索に比較して、やや成功率が落ちている。
単細胞モンテカルロ木探索の最大のメリットは、とにかくメモリを食わないことである。性能は、モンテカルロ木探索よりやや劣るが、予想以上の結果が出た。
ということは、このような不完全情報ゲームに対してモンテカルロ木探索を行った場合、不完全な部分がかなり支配的ならば、単細胞モンテカルロ木探索でも良いかも知れない。
ひとり遊び「計算」には、さらに難易度を上げた遊び方がある。
- コンピュータ:最初に台札を全然出さない。
- 超人:台札の山を3つにする。
コンピュータはやや難しくなる程度だが、超人は一気に難しくなる。
ここで紹介したモンテカルロ木探索でも、それらについて、ある程度の成功率を出すことができたが、技術的に特別なことは何もしていないので省略する。
とらんぷの一人遊び「計算」について、できるだけ安直に成功率の高い方法を検討しようということで、モンテカルロ木探索を行い、さらに単細胞モンテカルロ木探索なるものまで試した。
面倒でも良いから、もっと高い成功率を得たいと思った人は、あれこれ試してい欲しい。頑張れば99%以上の成功率が得られることは、第2回(9月16日公開)に書いていたので、それを参考にさらに研究を進めることも可能と思われる。
この連載は、コンピュータ囲碁の世界で有名になったモンテカルロ木探索を、別の世界でも効果があるのかどうかを試すことであった。結論は、まずまずの成果だった。めでたし、めでたしということで、連載を終了とする。



