MATH POWER 2017 向けに巨大パズル作成(10) 芋づる式
2017年 10月 04日
MATH POWER 2017で挑戦してもらう247合体ナンプレ関連についてあれこれ書いてきたが、もうイベントの日が間近だ。
ということで、合体ナンプレでしか経験できないような事を紹介しよう。
次の図の状態まで解き進んだとしよう。
まだ決まるところは色々あるのだが、非常に特徴的な決まり方がある。
それも、連続技といか、芋づる式というか、どんどん決まるのがある。
どんどん決まるのは、9x9の普通のナンプレでもあるのだが、この問題では、ある数字について、かなり広範囲に決まっていくので、次を見る前に、ぜひ自力で見つけてみよう。
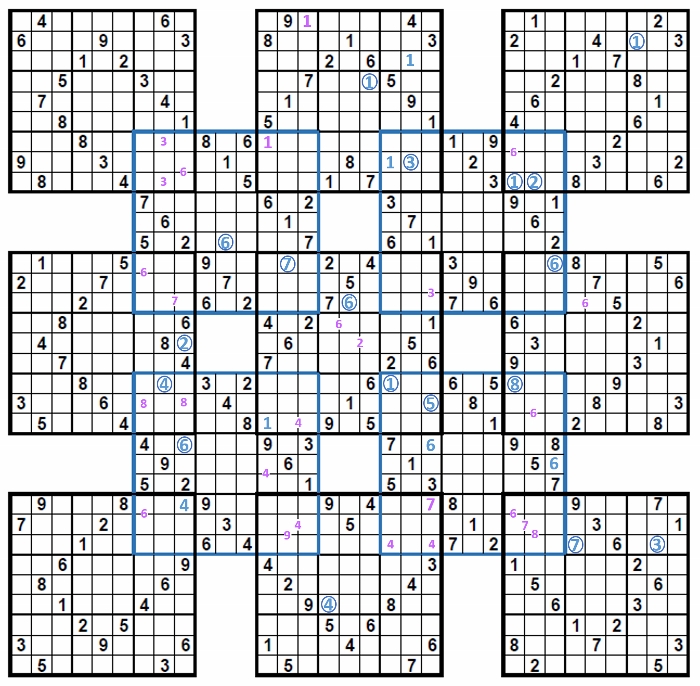 何が芋づる式かを以下に示す。
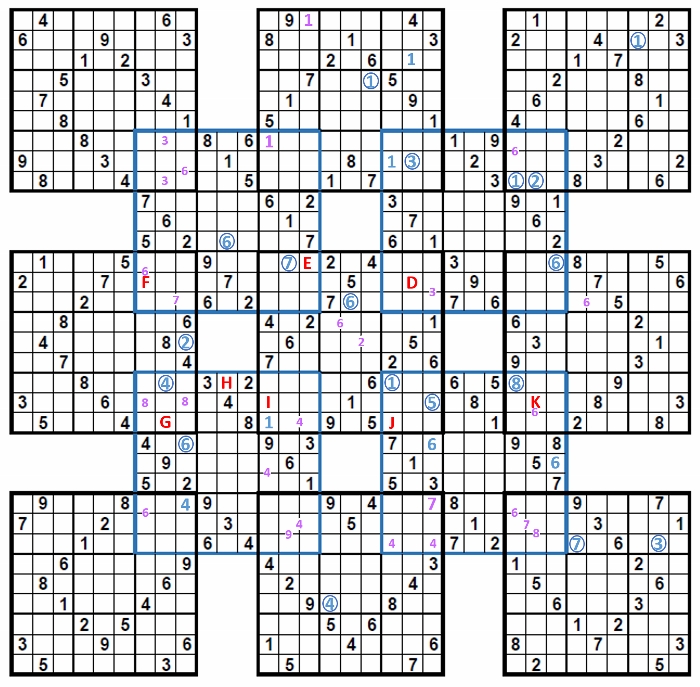
何が芋づる式かを以下に示す。
次図のD,E,F,G,H,I,J,Kの順番に一気に6が決まっていく。
13合体なので、縦、横にどんどん伸びていくというのはなく、芋づるがぐるぐる回る感じになるが、合体数が多くなると、上下左右にどんどん蔓がのびていくことがある。
つまり、はるか彼方に影響が出て数字が決まる。
このスケール感は、普通の9x9のナンプレでは全然味わうことができない。
 13合体でこのくらいの広がりがあるのだがから、247合体になったら一体どんな芋づる式がでてくるだろか。
13合体でこのくらいの広がりがあるのだがから、247合体になったら一体どんな芋づる式がでてくるだろか。
では、会場で、あるいは公式生放送ニコニコ動画で楽しもう。
ということで、合体ナンプレでしか経験できないような事を紹介しよう。
次の図の状態まで解き進んだとしよう。
まだ決まるところは色々あるのだが、非常に特徴的な決まり方がある。
それも、連続技といか、芋づる式というか、どんどん決まるのがある。
どんどん決まるのは、9x9の普通のナンプレでもあるのだが、この問題では、ある数字について、かなり広範囲に決まっていくので、次を見る前に、ぜひ自力で見つけてみよう。
 何が芋づる式かを以下に示す。
何が芋づる式かを以下に示す。13合体なので、縦、横にどんどん伸びていくというのはなく、芋づるがぐるぐる回る感じになるが、合体数が多くなると、上下左右にどんどん蔓がのびていくことがある。
つまり、はるか彼方に影響が出て数字が決まる。
このスケール感は、普通の9x9のナンプレでは全然味わうことができない。
 13合体でこのくらいの広がりがあるのだがから、247合体になったら一体どんな芋づる式がでてくるだろか。
13合体でこのくらいの広がりがあるのだがから、247合体になったら一体どんな芋づる式がでてくるだろか。では、会場で、あるいは公式生放送ニコニコ動画で楽しもう。




