円周上にN点を取り、任意の2点間の距離が整数の場合とは(3)
2018年 01月 14日
今まで、2点間の距離は整数としてきたが、2点間の距離を有理数でも良いことにしよう。
全ての2点間の距離が有理数であれば、全ての距離の分母の最小公倍数を掛けてしまえば、全ての2点間の距離を整数にできる。
ということで、「任意の2点間の距離が整数」でも「任意の2点間の距離が有理数」でも同じことである。
そこで、円をどんどん大きくしていくことを中止しよう。
つまり、円の大きさを一度決めたら、固定しても良いのだ。
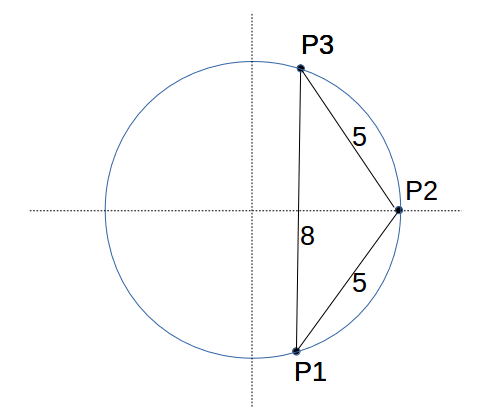
まず、右図のように、3:4:5 の直角三角形が2つ、長さ3の辺でつながったものを考えてみよう。
すると、辺の長さが 5:5:8 の二等辺三角形ができ、この三角形に外接する円を考える。
また、各頂点を図のように P1、P2、P3 とする。
つまり、P1ーP2 、P2ーP3 の距離は5である。
今回は、この距離5に注目する。
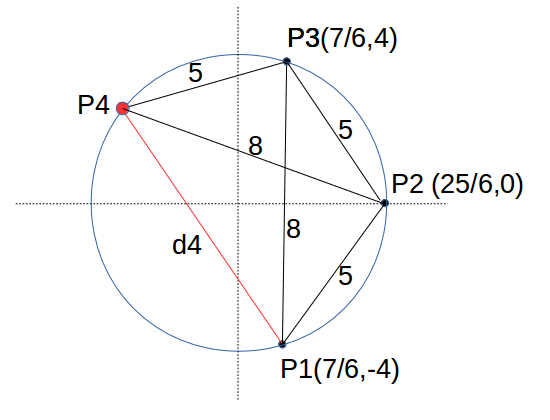
今までは、2点間の距離が整数にこだわっていたのだが、円の大きさをこのままにして、P3から距離5の頂点をP4とする。
 ここで突然だが、「トレミーの定理」を使う。
円周に内接する四角形に関する定理で、辺と対角線の長さに関する等式
ここで突然だが、「トレミーの定理」を使う。
円周に内接する四角形に関する定理で、辺と対角線の長さに関する等式
AC・BD = AD・BC + AB・DC
が成り立つ。(トレミーの定理/Wikipedia)
これを使うと、
8*8 = 5*5 + 5*d4
d4 = 39 / 5
となり、d4は有理数である。
全ての2点間の距離が有理数であれば、全ての距離の分母の最小公倍数を掛けてしまえば、全ての2点間の距離を整数にできる。
ということで、「任意の2点間の距離が整数」でも「任意の2点間の距離が有理数」でも同じことである。

そこで、円をどんどん大きくしていくことを中止しよう。
つまり、円の大きさを一度決めたら、固定しても良いのだ。
まず、右図のように、3:4:5 の直角三角形が2つ、長さ3の辺でつながったものを考えてみよう。
すると、辺の長さが 5:5:8 の二等辺三角形ができ、この三角形に外接する円を考える。
また、各頂点を図のように P1、P2、P3 とする。
つまり、P1ーP2 、P2ーP3 の距離は5である。
今回は、この距離5に注目する。

今までは、2点間の距離が整数にこだわっていたのだが、円の大きさをこのままにして、P3から距離5の頂点をP4とする。
すると、P1 P2 P3 P4 で決まる四角形(台形)ができる。
このとき、 d4 = P1ーP4の距離はいくらになるであろうか。
 ここで突然だが、「トレミーの定理」を使う。
円周に内接する四角形に関する定理で、辺と対角線の長さに関する等式
ここで突然だが、「トレミーの定理」を使う。
円周に内接する四角形に関する定理で、辺と対角線の長さに関する等式AC・BD = AD・BC + AB・DC
が成り立つ。(トレミーの定理/Wikipedia)
これを使うと、
8*8 = 5*5 + 5*d4
d4 = 39 / 5
となり、d4は有理数である。

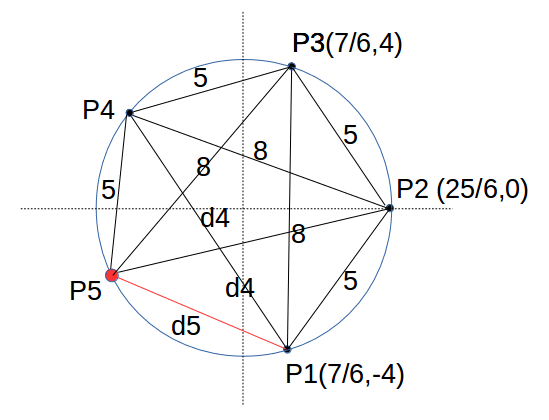
さらに、右図のようにP4から距離5の点をP5とする。
すると、d5=P1ーP5 だけが新しい距離で、それ以外の任意の2点間の距離は既出の距離(有理数)である。
ここで P1 P2 P3 P5 からなる四角形についてトレミーの定理を適用すると、
d4*8 = 5*8 + 5*d5
d5 = 112 / 25
となり、d5は有理数である。
というよりも、トレミーの定理で、一辺の長さが不明で、その他の長さが全部有理数だと、長さ不明の辺が有理数として求まる。
さて、P1, P2, P3, P4, P5, P6, … と延々と続けていくとどうなるであろうか。
新たにできる辺 dn = P1ーPn は必ず有理数になる。
そして、P1, P2, P3, P4, P5, P6, …の頂点は重ならないので(証明は省略)、半径25/6 の円周上に延々と距離5の点を取り続けることで、任意の2頂点間の距離を有理数にできる。
ということは、円が大きくなることを気にしなければ、円周上にいくらでも頂点を取り、任意の2頂点間の距離を整数にできる。
完



